正交时频空间调制(OTFS)技术详解:基础原理与未来挑战
正交时频空间(OTFS)调制将信息嵌入延迟-多普勒域,有效应对高速移动下的多普勒效应。相比OFDM,OTFS在高动态信道中具备全分集增益、低导频开销与强鲁棒性,是6G候选技术之一。
随着无线通信技术的快速发展,下一代无线网络面临着前所未有的挑战。这些网络需要支持越来越多样化的应用场景,包括飞机上的移动通信(MCA)、低地球轨道(LEO)卫星通信、高速列车通信系统、无人机(UAV)网络以及车对车(V2V)通信网络。这些应用场景的共同特点是存在高速相对运动,导致无线信道呈现快速时变特性,这主要是由多普勒效应引起的。
在高移动性传播环境中,如果系统设计时没有充分考虑多普勒效应,无线通信性能将会严重恶化。让我们通过一个具体的例子来理解这个问题的严重性。考虑一个工作在载频 $f_c = 3.5$ GHz 的OFDM系统,采用子载波间隔 $\Delta f = 15$ kHz,需要支持相对速度 $v = 300$ km/h 的移动通信。在这种情况下,最大多普勒频移为:
包含20%循环前缀的OFDM符号持续时间为 $T_{symbol} = 80$ ms。根据通信理论,信道的相干时间可以估算为:
这意味着在一个相干时间区间内最多只能容纳 $\lfloor 257.14/80 \rfloor = 3$ 个OFDM符号。换句线个OFDM符号就需要插入一个导频符号进行信道估计,这将导致至少33%的导频开销,严重降低了系统的频谱效率。
正是在这样的技术背景下,正交时频空间(OTFS)调制作为一种革命性的新型波形被提出。与传统的OFDM在时频(TF)域放置信息符号不同,OTFS将信息符号放置在延迟-多普勒(DD)域中。这个看似简单的改变带来了根本性的优势:在DD域中,即使是快速时变的无线信道也呈现出准静态和稀疏的特性。这是因为DD域直接反映了散射体的物理特性——只有当散射体的位置或速度发生剧烈变化时,DD域信道响应才会改变。
OTFS调制主要有两种实现架构:基于辛有限傅里叶变换(SFFT)的方法和基于离散Zak变换(DZT)的方法。这两种方法虽然在实现细节上有所不同,但在某些条件下可以得到相同的输入输出关系。
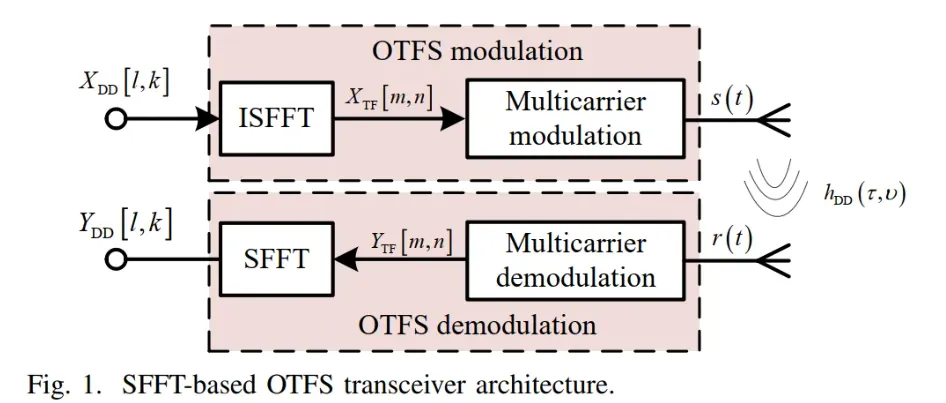
图1展示了完整的SFFT-based OTFS收发机系统框图。该架构可以分为发送端和接收端两个主要部分:
图中虚线框标识了OTFS调制和解调的核心部分,展示了其与传统OFDM系统的兼容性——OTFS可以看作在OFDM基础上增加了DD域到时频域的变换。
发送端的信号处理包括两个关键步骤。首先是逆辛有限傅里叶变换(ISFFT),将DD域符号映射到时频域:
其中 $g_{tx}(t)$ 是发送端脉冲成形滤波器,它决定了信号在时频域的局部化特性。
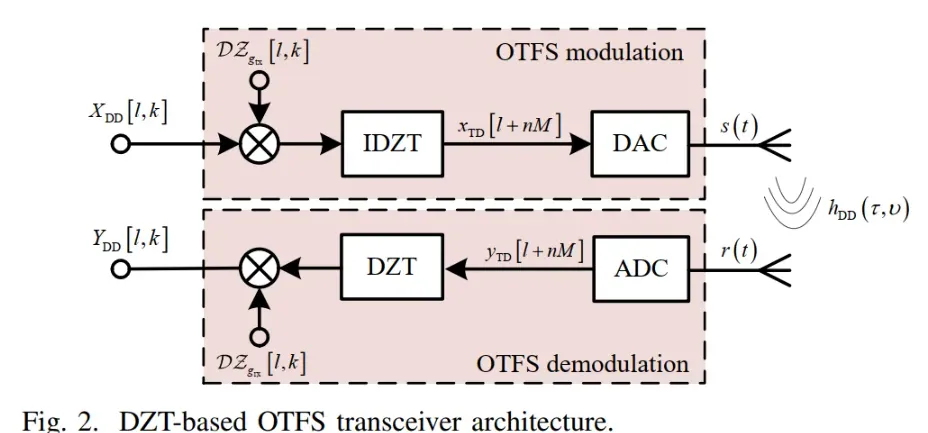
图2展示了DZT-based OTFS的系统框图,其核心特点是直接在DD域和时域之间进行变换,绕过了时频域:
相比SFFT架构,DZT架构的主要优势在于计算复杂度更低,因为它避免了时频域的中间变换步骤。
离散Zak变换建立了一维序列和二维序列之间的映射关系。对于周期为 $MN$ 的序列 $x$,其离散Zak变换定义为:
这个变换具有重要的物理意义:它将时域序列 $x[l+nM]$ 分解为 $M$ 个子序列(由索引 $l$ 标识),然后对每个子序列进行 $N$ 点DFT(由索引 $k$ 标识)。
尽管SFFT和DZT架构在实现方式上有所不同,但它们在特定条件下是等价的。特别是,当采用矩形发送和接收滤波器,且延迟和多普勒频移都是整数时,两种方法得到完全相同的DD域输入输出关系:
延迟-多普勒域的概念源于雷达信号处理和无线信道建模。在雷达系统中,目标的距离和速度分别对应于延迟和多普勒参数。类似地,在无线通信中,每个传播路径可以用其延迟(反映传播距离)和多普勒频移(反映相对运动)来表征。
从数学角度看,DD域提供了一种描述线性时变系统的自然框架。考虑一个时变系统,其冲激响应为 $h(t,\tau)$,其中 $t$ 是观察时间,$\tau$ 是延迟。通过对时间变量进行傅里叶变换,我们得到DD域表示:
这个变换揭示了系统的时变特性:$\nu$ 参数量化了系统随时间的变化率。
OTFS调制的核心创新在于直接在DD域嵌入信息。每个DD域信息符号 $X_{DD}[l,k]$ 被调制到一个DD域基函数上,这个基函数在时域表现为时变载波信号。具体而言,位于 $(l_0,k_0)$ 位置的DD域冲激对应的时域信号为:
DD域的分辨率受到海森堡不确定性原理的限制。延迟分辨率和多普勒分辨率之间存在基本的权衡关系:
这意味着增加帧中的资源元素数量 $MN$ 可以提高DD域的联合分辨率,但延迟和多普勒的单独分辨率仍受到带宽和时间持续的限制。
将连续DD域信道离散化到OTFS网格上是一个关键步骤。离散DD域信道响应可以表示为:
对于整数延迟和多普勒($l_i,k_i \in \mathbb{Z}$)以及理想的矩形滤波器,采样函数简化为:
实际系统中,路径延迟和多普勒频移通常不是网格间隔的整数倍,导致分数延迟和分数多普勒问题。在这种情况下,采样函数变得更加复杂:
这个表达式涉及模糊函数 $A{g{tx}g_{rx}}(\tau,\nu)$,它量化了发送和接收滤波器对不同延迟-多普勒偏移的响应:
分数多普勒的存在破坏了DD域的正交性,导致符号间干扰(ISI)和载波间干扰(ICI)。这是OTFS系统设计中的一个主要挑战。
OTFS调制的一个关键优势是每个DD域符号都经历整个时频域信道响应。这可以从输入输出关系中看出——每个发送符号 $X{DD}[l,k]$ 通过信道矩阵 $H{DD}$ 影响所有接收符号。这种二维扩展使得OTFS能够获取时间和频率维度的全部分集增益。
分集增益可以定量分析。对于具有 $L$ 个独立多径的信道,传统OFDM在一个符号周期内只能获取频率分集,分集阶数为 $L$。而OTFS通过 $N$ 个时隙的扩展,理论上可以获得 $NL$ 的分集阶数,显著提高了可靠性。
在DD域中,信道响应是稀疏的——只有 $P$ 个非零元素,其中 $P \ll MN$。这种稀疏性可以被利用来大幅降低信道估计的导频开销。具体而言,根据压缩感知理论,所需的导频数量大约为:
相比之下,OFDM系统需要的导频数量与信道长度成正比,在高移动性场景下可能需要频繁的导频插入。
OTFS的循环卷积结构使其对多普勒扩展具有内在的鲁棒性。多普勒频移在DD域中表现为循环移位,不会破坏符号的正交性(在整数多普勒情况下)。这与OFDM形成鲜明对比,在OFDM中,即使很小的多普勒扩展也会导致严重的ICI。
定量分析表明,对于归一化多普勒扩展 $\nu_{max}T 0.1$,OFDM的性能急剧下降,而OTFS仍能保持良好的性能。这使得OTFS特别适合于高速移动场景。
辛有限傅里叶变换(SFFT)源于辛几何和时频分析理论。考虑希尔伯特空间 $L^2(\mathbb{R})$ 上的位移算子:
对于有限维情况,考虑 $\mathbb{C}^{MN}$ 空间,离散位移算子定义为:
这表明 $\phi_{l,k}$ 是位移算子的特征向量,SFFT就是向这组特征向量的投影。
考虑整数延迟 $l_i$ 和整数多普勒 $k_i$ 的情况。DD域基函数经过信道后的变换为:
对于根升余弦(RRC)脉冲,模糊函数的计算更为复杂,通常需要数值方法。但RRC脉冲可以提供更好的带外抑制和更低的ISI/ICI。
考虑独立同分布瑞利衰落信道,每条路径的增益 $h_i \sim \mathcal{CN}(0,1/P)$。OTFS系统的成对错误概率(PEP)可以通过计算错误事件的欧氏距离来分析。
其中 $\mathbf{H}$ 是循环卷积矩阵。通过Chernoff界和矩生成函数方法,平均PEP为:
这表明OTFS可以获得分集阶数 $r$,在最佳情况下 $r = \min(MN,PL)$,其中 $L$ 是每条路径的时延扩展(以采样点计)。
消息传递(MP)算法在OTFS检测中广泛使用。考虑因子图表示,其中变量节点表示DD域符号,因子节点表示观测。消息更新规则为:
收敛性取决于因子图的结构。对于整数延迟和多普勒,因子图是无环的,MP算法保证收敛到精确的边缘后验概率。但对于分数多普勒,因子图包含短环,导致:
OTFS调制技术革新无线通信,将信息从时频域迁移至时延-多普勒域,利用信道的准静态特性与稀疏性,显著提升高速移动场景下的抗多普勒性能与频谱效率,成为6G关键候选技术。
正交时频空间(OTFS)调制技术在延迟-多普勒域进行信号设计,有效应对高多普勒、短包传输等5G挑战。相比传统OFDM,OTFS通过全时频分集和信道硬化,显著提升高速移动场景下的鲁棒性与分集增益,仿真显示其在BLER性能上可获得3-4dB SNR增益,尤其适用于车联网、物联网等应用场景。
双选择性信道下正交啁啾分复用(OCDM)的低复杂度均衡算法研究——论文阅读
本文提出统一相位正交啁啾分复用(UP-OCDM)方案,利用循环矩阵特性设计两种低复杂度均衡算法:基于带状近似的LDL^H分解和基于BEM的迭代LSQR,将复杂度由$O(N^3)$降至$O(NQ^2)$或$O(iNM\log N)$,在双选择性信道下显著提升高频谱效率与抗多普勒性能。
本文提出一种基于连续相位频移键控(CPFSK)的新型雷达信号设计方法,通过确保频率切换时相位连续,有效抑制频谱旁瓣与能量泄漏。相比传统FSK信号,该方法在不牺牲脉冲压缩性能的前提下,实现旁瓣降低约20dB,显著提升频谱利用效率,适用于复杂电磁环境下的高性能雷达系统。
正交时频空(OTFS)调制通过延迟-多普勒域传输,将高多普勒信道转化为准静态环境,显著提升高速移动下的通信鲁棒性。本文研究其信号检测与信道估计,提出低复杂度MCMC检测算法和基于PN导频的稀疏信道估计算法,验证了OTFS在高速场景下的优异性能。
本文综述正交时频空间(OTFS)技术,一种面向6G高移动性场景的新型延迟-多普勒域通信范式。OTFS通过在延迟-多普勒域调制信号,克服传统OFDM在高速移动下的多普勒扩展难题,具备信道稳定性强、抗干扰能力优、峰均比低等优势。文章系统阐述OTFS的信道模型、调制原理、收发机设计、ISAC一体化及在卫星、水声、可见光等新兴场景的应用前景,为其在6G空天地海一体化网络中的应用提供理论支撑与技术路径。
本文提出基于离散Zak变换(DZT)的正交时频空间(OTFS)调制新方法,通过DZT统一构建OTFS收发框架,揭示其在时延-多普勒域的输入输出关系,简化系统分析并深化对分辨率与脉冲设计的理解,为高移动性通信提供高效解决方案。
基于BP神经网络的CoSaMP信道估计算法matlab性能仿真,对比LS,OMP,MOMP,CoSaMP
本文介绍了基于Matlab 2022a的几种信道估计算法仿真,包括LS、OMP、NOMP、CoSaMP及改进的BP神经网络CoSaMP算法。各算法针对毫米波MIMO信道进行了性能评估,通过对比不同信噪比下的均方误差(MSE),展示了各自的优势与局限性。其中,BP神经网络改进的CoSaMP算法在低信噪比条件下表现尤为突出,能够有效提高信道估计精度。
Julia,一款高性能的开源编程语言,专为科学计算设计,具备动态高级语言特性,速度快,无需解释器。支持多种平台,包括macOS、Windows和Linux等。其特点是小核心、丰富的类型语法、高性能、并行计算优化、C函数直接调用、Unicode支持及元编程工具。常用于数值计算。首个Julia程序示例为打印Hello World!。参考链接:[Julia官网](和[Julia中文手册](。

